Codeforces泛做

文章最后更新时间为：2021 年 05 月 02 日 18:00:44

由于 $\text{EC Final 2021}$ 打铁了，所以随便做做 $\text{CF}$ 上的题。

CF1514C Product 1 Modulo N

首先选出来的数必须是和, 那么直接把所有与 $N$ 互质的数乘起来模 $N$，如果结果为 $1$，那么直接输出；否则去掉这个结果输出其他的数.

复杂度$O(N\log N)$.

CF1514D Cut and Stick

记 $[l,r]$ 这个区间出现过次数最多的数的出现次数为 $x$.

如果 $x\times 2$ 小于区间长度直接输出 $1$，否则输出 $2\times x-(r-l+1)$.

但实际上并不需要求区间众数，因为一个区间内最多只有一个数满足它出现的次数 $\times 2$ 大于等于区间长度, 所以可以直接在主席树上二分就好，找不到这个数输出 $1$, 找到就输出 $2\times x-(r-l+1)$.

时间复杂度$O((n+q)\log n)$，空间复杂度$O(n\log n)$.

Code

CF1514E Baby Ehab's Hyper Apartment

很有意思的一道题，首先有一个结论: 这个有向图上一定有一条哈密顿路径 (从一个点出发, 经过每个点一次). 证明如下：

一开始点集为 $[n]$，每次将其划分成两个等大的子集，直到集合的大小为 $1$，那么显然这个点本身组成的路径就是这个点集的哈密顿路径. 然后考虑合并两个点集的哈密顿路径，如图：

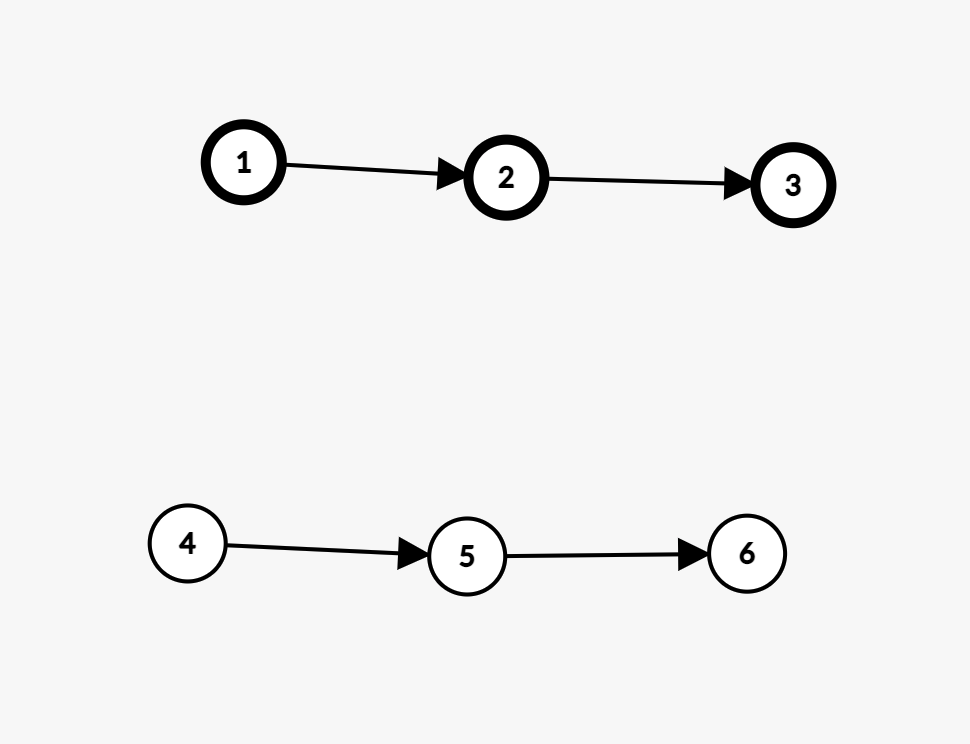
点集 $\{1,2,3\}$ 的哈密顿路径为 $1\to 2\to 3$，而点集 $\{4,5,6\}$ 的哈密顿路径为 $4\to 5\to 6$. 我们可以认为这里$a\to b$ 的边代表 $a<b$，然后通过双指针合并这两个递增的序列，假如最后合并完的序列为：$1\ 4\ 5\ 2\ 3\ 6$，那么必然存在一条哈密顿路径就是 $1\to 4\to 5\to 2\to 3\to 6$.

整个过程可以看成一个 $\text{merge_sort}$，其中的每一次比较对应了一次第一类询问，而 $\text{merge_sort}$ 中只有 $O(n\log n)$ 次比较，所以第一类询问的次数不超过 $O(n\log n)$. 也就是说我们可以在 $9n$ 次第一类询问内求出一条哈密顿路径.

假如我们求出来了一条哈密顿路径，那么这条哈密顿路径前面的点一定可以到达后面的点，所以我们只关心后面的点能不能到达前面的点，考虑用双指针实现，最初有两个指针 $l,r$ 都等于 $n$ (即代表这条哈密顿路径上的最后一个点)，每次查询是否存在一条边由 $r$ 到 $[1,l-1]$ 中的一个点，如果存在将 $l$ 的值减 $1$，否则说明 $[l,r]$ 中的点可以互相到达，但是 $r$ 不能到达 $l$ 之前的点，所以将 $r$ 的值减 $1$，然后重复上述过程。直到 $r$ 小于 $l$，说明 $[l,n]$ 中的点无法到达 $[1,r]$ 中的点；然后将 $l$ 的值减 $1$ 再继续重复上述过程。 因为两个指针一共只会移动 $2\times n$ 次，故第二类询问的次数不超过 $2\times n$，至此问题被完美解决.

复杂度 $O(n\log n+n^2)$.

Code

CF1516B AGAGA XOOORRR

记所有的数异或起来为 $x$：

• 如果$x=0$，那么最后一定可以将序列缩成两个相同的数.
• 否则，最终的序列一定是有奇数个数，并且所有的数都为$x$. 那么直接 $\text{check}$ 一下能不能划分即可.

复杂度 $O(n)$.

Code

CF1516C Baby Ehab Partitions Again

首先用背包求出是否有解，如果有解，那我们令 $k$ 为使得下式成立的最大的 $k$：

$$ \forall i\in[n], 2^k\mid a_i $$

那我们只要删除一个满足 $\frac{a_i}{2^k}$ 是奇数的 $i$ 即可.

复杂度 $O(n\sum a)$.

Code

CF1516D Cut

首先 $[l,r]$ 内的数满足 $\prod_{i=l}^ra_i=\operatorname{lcm}(a_l,a_{l+1},\cdots,a_r)$ 等价于每个质因子只在 $[l,r]$ 中的一个数中出现.

考虑设 $f_{i,j}$ 表示从 $i$ 开始划分 $2^j$ 段后最多能到的位置的下一个，那么有递推式：

$$ f_{i,j}=f_{f_{i,j-1},j-1} $$

那么如何求解边界 $f_{i,0}$ 呢？考虑设 $g_{i,p}=\min\{x\mid x>i,p\mid a_x\}$，$r_i$ 为最大的使得 $[i,r_i]$ 内的数满足 $\operatorname{lcm}$ 等于乘积的数. 那么则有：

$$ r_i=\min\{r_{i+1},\min_{p\mid a_i}\{g_{i,p}-1\}\} $$

且 $f_{i,0}=r_i+1$. 倒着递推即可完美解决这个问题. 然后关于答案求解则是倍增数组的经典应用，在此不多做赘述.

复杂度 $O((n+q)\log n)$.

Code

CF1516E Baby Ehab Plays with Permutations

令 $f_{i,j}$ 表示用最少 $j$ 次 $\text{swap}$ 可以把多少种长度为 $i$ 的错排还原. 那么有：

$$ f_{i,j}=f_{i-1,j-1}\times(i-1) + f_{i-2,j-1}\times (i-1) $$

这个转移的组合意义为：

• $i$ 和前 $i-1$ 个数里的任意一个组成一个大小为 $2$ 的新环. ($f_{i-2,j-1}\times (i-1)$)
• 将 $i$ 插入到前 $i-1$ 个数中组成的已经存在的环里. ($f_{i-1,j-1}\times (i-1)$)

那么令 $g_i$ 表示用最少 $i$ 次 $\text{swap}$ 可以把多少种长度为 $n$ 的排列还原，那么有：

$$ g_i=\sum_{j=2}^{2\times k} \binom{n}{j}f_{j,i} $$

令 $h_i$ 表示用 $i$ 次 $\text{swap}$ 可以把多少种长度为 $n$ 的排列还原，那么有：

$$ h_i=\begin{cases} 0,&i=0\\ \sum_{j=0}^{\left\lfloor \frac{i}{2}\right\rfloor} g_{i-2j},&i>1 \end{cases} $$

复杂度 $O(k^2)$.

Code