Set Theory

文章最后更新时间为：2021 年 03 月 14 日 12:01:12

I have learnt a little about set theory in discrete mathematics. This post is my studying note.

Sets

DEFINITION: A set is an unordered collection of objects(elements).

A set contains its elements; $a\in A(a\not\in A):a$ is (not) an element of $A$.
Describe a set:
- $\textbf{roster method}_{\text{列举法}}$: enumerate the elements of set.
  - $\{1,2,\{3,4,\{5\}\}\}$
- $\textbf{set builder}_{\text{构造法}}:\{a:P(a)\}(\text{or }\{a\mid P(a)\})$
  - $A=\{x\mid x>1\}$
empty set: the set that has no element.(null set, $\emptyset$)
universal set: the set which contains all objects under consideration
$A=B:\forall x(x\in A\leftrightarrow x\in B )$ --- $A$ is equal to $B$
$A\subseteq B:\forall x(x\in A\to x\in B)$ --- $A$ is a subset of $B$
$A\subset B:(A\subseteq B)\land (A\ne B)$ --- $A$ is a $\textbf{proper subset}_{\text{真子集}}$ of $B$.

Set Operations

DEFINITION: Let $A,A_1,...,A_n,B,C,S$ be any sets. Let $U$ be a universal set.

$A\cup B=\{x\mid x\in A\lor x\in B\}:$ the $\textbf{union}_{\text{并集}}$ of $A$ and$B$
$A\cap B=\{x\mid x\in A\land x\in B\}:$ the $\textbf{intersection}_{\text{交集}}$ of $A$ and$B$
- $\textbf{disjoint}_{\text{不交}}:$ $A\cap B=\emptyset$
$A-B=\{x\mid x\in A\land x\not\in B\}:$ the $\textbf{difference}_{\text{相对补集}}$ of $A$ and $B$
- the complement of $B$ with respect to $A$
$A\oplus B=(A-B)\cup (B-A):$ the $\textbf{symmetric difference}_{\text{异或}}$ of $A$ and $B$
$\mathcal{P}(A)=\{x\mid x\subseteq A\}:$ the $\textbf{power set}_{\text{幂集}}$ of $A$
$A\times B=\{(a,b)\mid a\in A\land b\in B\}:$ the $\textbf{Cartesian product}_{\text{笛卡尔积}}$ of $A$ and $B$
- $A_1 \times \cdots \times A_n=\{(a_1,..., a_n)\mid a_1\in A_1\land \cdots \land a_n\in A_n\}$
  - Specially let $A^n$ denote $\begin{matrix}\underbrace{A\times \cdots \times A}\\n\end{matrix}$
$\overline{A} = \{x\in U\land x\not\in A\}$: the $\textbf{complement}_{\text{补集}}$ of $A$
- $\overline{A}=U-A$

Gneralized union : $\cup A=\{x\mid \exist y(y\in A\land x\in y)\}$ --- $A$ is a set of sets

$\cup\left\{A_{1}, A_{2}, \ldots, A_{n}\right\}=\bigcup_{i=1}^{n} A_{i}$
$\cup\left\{A_{1}, A_{2}, \ldots\right\}=\bigcup_{i=1}^{\infty} A_{i}$
$\cup\left\{A_{i}: i \in I\right\}=\bigcup_{i \in I} A_{i}$
$\cup \emptyset=\emptyset$

Gneralized intersection : $\cap A = \{x\mid \forall y(y\in A\to x\in y)\}$

$\cap\left\{A_{1}, A_{2}, \ldots, A_{n}\right\}=\bigcap_{i=1}^{n} A_{i}$
$\cap\left\{A_{1}, A_{2}, \ldots\right\}=\bigcap_{i=1}^{\infty} A_{i}$
$\cap\left\{A_{i}: i \in I\right\}=\bigcap_{i \in I} A_{i}$
$\cap \emptyset$ is not meaningful

Laws of Set Operations

Function

DEFINITION : Let $A,B\ne \emptyset$ be two sets.

A $\textbf{function(map)}_{\text{函数(映射)}}$ $f:A\to B$ assigns a unique element $b\in B$ for every $a\in A$.
- $f(a)=b$ : $b$ is the $\textbf{image}_{\text{象}}$ of $a$ and $a$ is a $\textbf{preimage}_{\text{原象}}$ of $b$.
- $A$ is the $\textbf{domain}_{定义域}$ of $f$ and $B$ is the $\textbf{codomain}_{陪域}$ of $f$.
The image of $X\subseteq A$ is $f(X)=\{t\mid \exist x\in X(f(x)=t)\}$. The preimage of $Y\subseteq B$ is $f^{-1}(Y)=\{x\mid x\in A\land f(x)\in Y\}$. The $\textbf{range}_{\text{值域}}$ of $f$ is $f(A)$.
$f:A\to B$ is said to be
- $\textbf{injective}_{\text{单射}}(\text{one-to-one})$ if $f(a)=f(b)\Rightarrow a=b$
- $\textbf{surjective}_{\text{满射}}(\text{onto})$ if $f(A)=B$
- $\textbf{bijective}_{\text{双射}}$ if it is injective and surjective(one-to-one and onto).
$g:A\to B$ and $f:B\to C$, $(f\circ g)(x)=f(g(x))$ is the $\textbf{composition}_{\text{复合}}$ of $f,g$.
If $f:A\to B$ is a bijection, then $f$ has an $\textbf{inverse function}_{\text{反函数}}\ \ f^{-1}:B\to A$.

$\textbf{Cardinality}_{基数}$ of Sets

DEFINITION : Let $A$ be a set.

$A$ is called a $\textbf{finite set}_{\text{有限集}}$ if it has finitely many elements.
- The $\textbf{cardinality}_{基数}\ |A|$ of a finite set $A$ is the number of elements in $A$.
$A$ is called an $\textbf{infinite set}_{无限集}$ if it is not a finite set.

EXMAPLE : $\emptyset, \{1\}, \{x\mid x^2-2x-3=0\},\{a,b,c,...,z\}$ are all finite sets, $\mathbb{N}_{\text{自然数集}},\mathbb{Z}_{\text{整数集}},\mathbb{Q}_{\text{有理数集}},\mathbb{R}_{\text{实数集}},\mathbb{C}_{\text{复数集}}$ are all infinite sets.

DEFINITION : Let $A,B$ be any sets.

$A,B$ $\textbf{have the same cardinality}_{\text{等势}}(\color{red}{|A|=|B|})$ if there exists a bijection $f:A\to B$
We say that $\color{red}{|A|\le |B|}$ if there exists an injection $f:A\to B$
- If $|A|\le |B|\land |A|\ne |B|$ , we sat thay $\color{red}{|A|<|B|}$

THEOREM : Let $A,B,C$ be any sets. Then

$|A|=|A|$
$|A|=|B|\Rightarrow |B|=|A|$
$|A|=|B|\land |B|=|C|\Rightarrow |A|=|C|$
$|A|\le |B|\land |B|\le |A|\Rightarrow |A|=|B|$ (Schröder-Bernstein Theorem)

EXMAPLE : $|\mathbb{Z}^+|=|\mathbb{N}|=|\mathbb{Z}|=|\mathbb{Q}^+|=|\mathbb{Q}|$

$f:\mathbb{Z}^+\to \mathbb{N}\ \ x\mapsto x-1$ (bijective)
$f:\mathbb{Z}\to \mathbb{N} \ \ f(x)=\begin{cases}2x&x\ge 0\\-(2x+1)&x<0\end{cases}$ (bijective)
$|\mathbb{Z}^+|=|\mathbb{Q}^+|$
- $f:\mathbb{Z}^+\to \mathbb{Q}^+\ \ x\mapsto x$ (injective)
- $g:\mathbb{Q}^+\to \mathbb{Z}^+\ \ \frac{p}{q}(p\in \mathbb{Z}^+,q\in \mathbb{Z}^+)\mapsto \frac{(p+q-1)(p+q-2)}{2}+p$ (injective)
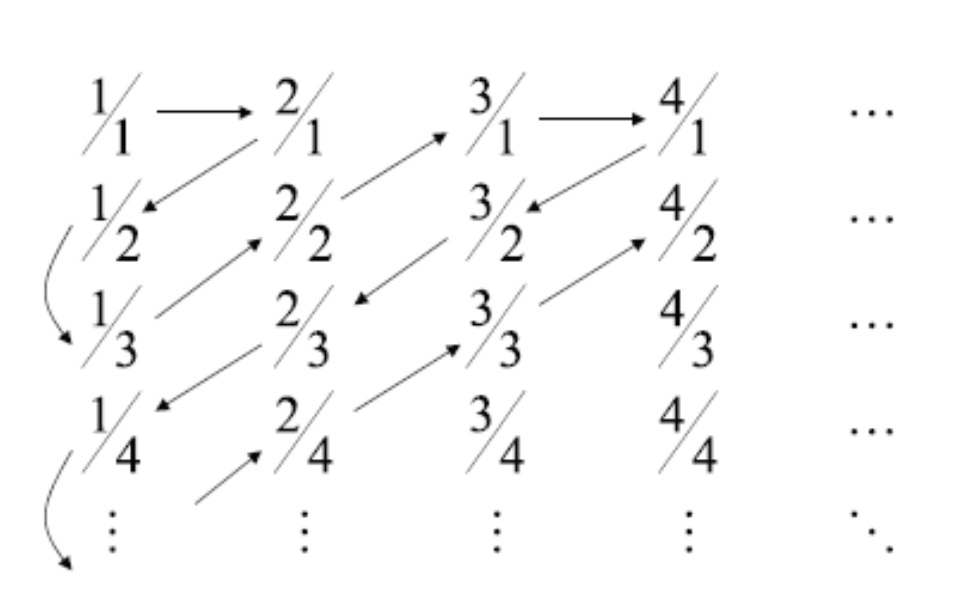
- Accroding to Schröder-Bernstein Theorem $|\mathbb{Z}^+|=|\mathbb{Q}^+|$
$|\mathbb{Q}^+|=|\mathbb{Q}|$
- $f:\mathbb{Z}\to \mathbb{Q}\ \ x\mapsto x$
- $g:\mathbb{Q}\to\mathbb{Z} \ \ g\left(\frac{p}{q}\right)=\begin{cases}\frac{(p+q-1)(p+q-2)}{2}+p&\frac{p}{q}>0\\0&p=0\\-\frac{(|p|+|q|-1)(|p|+|q|-2)}{2}-|p|&\frac{p}{q}<0\end{cases}$ (injective)
- $|\mathbb{Q}|=|\mathbb{Z}|=|\mathbb{Z}^+|=|\mathbb{Q}^+|$

EXMAPLE : $|\mathbb{R}^+|=|\mathbb{R}|=|(0,1)|=|[0,1]|$

$f:\mathbb{R}\to \mathbb{R}^+\ \ x\mapsto 2^x$ (bijective)
$f:(0,1)\to \mathbb{R}\ \ x\mapsto \tan\left({\pi}\left(x-\frac{1}{2}\right)\right)$ (bijective)
$f:[0,1]\to (0,1)$
- $f(1)=2^{-1},f(0)=2^{-2},f(2^{-n})=2^{-n-2},n=1,2,3,\cdots$
- $f(x)=x\text{ for other } x$
- bijective

EXAMPLE : $\left|2^X\right|=|\mathcal{P}(X)|$

$2^{X}=\{\alpha\mid \alpha:X\to \{0,1\}\text{ is a function}\}$ , the set of all functions from $X$ to $\{0,1\}$
$\mathcal{P}(X)=\{A\mid A\subseteq X\}$, the power set of $X$
$f:2^X\to \mathcal{P}(X)\ \ \alpha\mapsto A=\{x\mid \alpha(x)=1\}$ (bijective)

THEOREM : $|(0,1)|>|\mathbb{Z}^{+}|$

$g:\mathbb{Z}^+\to \mathbb{R}\ \ x\mapsto x$ (injective), $|\mathbb{Z}^+|\le |\mathbb{R}|=|(0,1)|$
Suppose that $|\mathbb{Z}^+|=|(0,1)|$, then there exists a bijection $f:\mathbb{Z}^+\to (0,1)$

$$ f(1)=0.b_{11}b_{12}b_{13}b_{14}b_{15}b_{16}b_{17}b_{18}b_{19}\cdots\\ f(2)=0.b_{21}b_{22}b_{23}b_{24}b_{25}b_{26}b_{27}b_{28}b_{29}\cdots\\ f(3)=0.b_{31}b_{32}b_{33}b_{34}b_{35}b_{36}b_{37}b_{38}b_{39}\cdots\\ f(4)=0.b_{41}b_{42}b_{43}b_{44}b_{45}b_{46}b_{47}b_{48}b_{49}\cdots\\ f(5)=0.b_{51}b_{52}b_{53}b_{54}b_{55}b_{56}b_{57}b_{58}b_{59}\cdots\\ f(6)=0.b_{61}b_{62}b_{63}b_{64}b_{65}b_{66}b_{67}b_{68}b_{69}\cdots\\ \cdots\\ f(n)=0.b_{n1}b_{n2}b_{n3}b_{n4}b_{n5}b_{n6}b_{n7}b_{n8}b_{n9}\cdots\\ \cdots $$

Let $b_i=\begin{cases}0,&b_{ii}\ne 0\\1,&b_{ii}=0\end{cases}$
$b=0.b_{1}b_{2}b_{3}b_{4}b_{5}\cdots$ is in $(0,1)$ but has no preimage
- $b\ne f(i)$ for every $i=1,2,3,...$
$f$ cannot be a bijection, and this gives contradiction
So $|(0,1)|\ge |\mathbb{Z}^+|\land |(0,1)|\ne|\mathbb{Z}^+|\Rightarrow |(0,1)|>|\mathbb{Z}^+|$

Contor's THEOREM : Let $A$ be any set. Then $|A|<|\mathcal{P}(A)|$.

$|A|\le |\mathcal{P}(A)|$
- $f:A\to \mathcal{P}(A)\ \ f(a)=\{a\}$ (injective)
$|A|\ne|\mathcal{P}(A)|$
- Assume that there is a bijection $g:A\to \mathcal{P}(A)$
- Define $X=\{a\mid a\in A\land a\not\in g(a)\}$
- $X$ should be in $\mathcal{P}(A)$. It is clear that $X\subseteq A$, hence $X\in \mathcal{P}(A)$
- Suppose that $X=g(x)$ for some $x\in A$
  - If $x\in X$, then $x\not\in g(x)=X$
    - This gives contradiction
  - If $x\not\in X$, then $x\in g(x)=X$
    - This gives contradiction
  - $X$ is not in $\mathcal{P}(A)$
- So there does not exist a bijection between $A$ and $\mathcal{P}(A)$

DEFINITION : A set $A$ is $\textbf{countalble}_{\text{可数, 可列}}$ if and only if $|A| < \infty\text{ or }|A|=|\mathbb{Z}^+|$; otherwise, it is said to be $\textbf{uncountable}_{\text{不可数,不可列}}$.

countably infinite: $|A|=|\mathbb{Z}^+|$

EXAMPLE :

$\mathbb{Z}^{-}, \mathbb{Z}^{+}, \mathbb{Z}, \mathbb{Q}^{-}, \mathbb{Q}^{+}, \mathbb{Q}, \mathbb{N}, \mathbb{N} \times \mathbb{N}$ are countable
$\mathbb{R}^{-}, \mathbb{R}^{+}, \mathbb{R},(0,1),[0,1],(0,1],[0,1),(a, b),[a, b]$ are uncountable

THEOREM : A set $A$ is countably infinite if and only if its elements can be arranged as a sequence $a_1,a_2,\cdots$

If $A$ is countably infinite, then there is a bijection $f:\mathbb{Z}^+\to A$
- $a_i=f(i)\text{ for every }i=1,2,3,\cdots$
If $A=\{a_1,a_2,\cdots\}$, then the bijective function $f:\mathbb{Z}^+\to A$ defined by $f(i)=a_i$

THEOREM : Let $A$ be countably infinite, then any infinite subset $X\subseteq A$ is countable.

Let $A=\{a_1,a_2,\cdots\}$. Then $X=\{a_{i_1},a_{i_2},\cdots\}$
- $X$ is countable

THEOREM : Let $A$ be uncountable, then ant set $X\supseteq A$ is uncountable.

Suppose that $X$ is countable, accroding to the previous THEOREM $A$ is countable.

THEOREM : If $A,B$ are countably infinite, then so is $A\cup B$

$A=\{a_1,a_2,a_3,\cdots\}, B=\{b_1,b_2,b_3,\cdots\}$
$A\cup B=\{a_1,b_1,a_2,b_2,\cdots\}$ // no elements will be included twice

THEOREM : If $A,B$ are countably infinite, then so is $A\times B$

$A=\{a_1,a_2,a_3,\cdots\}, B=\{b_1,b_2,b_3,\cdots\}$
$A \times B=\left\{\left(a_{1}, b_{1}\right),\left(a_{1}, b_{2}\right),\left(a_{2}, b_{1}\right),\left(a_{1}, b_{3}\right),\left(a_{2}, b_{2}\right),\left(a_{3}, b_{1}\right),\left(a_{1}, b_{4}\right), \ldots\right\}$

EXAMPLE : $|\mathcal{P}(\mathbb{Z}^+)|=|[0,1)|$

$|\mathcal{P}(\mathbb{Z}^+)|\le |[0,1)|$
- $f:\mathcal{P}(\mathbb{Z}^+)\to [0,1)\ \ \ \{a_1,a_2,\cdots\}\mapsto \sum\limits_{i}10^{-a_{i}}$ is an injection.
$|[0,1)|\le |\mathcal{P}(\mathbb{Z}^+)|$
- $\forall x\in [0, 1), x = 0.r_1r_2\cdots(r_1,r_2,\cdots\in\{0,...,9\},\text{no}\ \dot{9})$
  - $0\leftrightarrow 0000,1\leftrightarrow 0001,...,9\leftrightarrow 1001$
  - $x$ has a binary representation $x=0.b_1b_2\cdots$
    - $g:[0,1)\to \mathcal{P}(\mathbb{Z}^+)\ x\mapsto \{i\mid i\in Z^+\land b_i=1\}$ is an injection

$\textbf{Cardinal Arithmetic}_{\text{基数算术}}$

DEFINITION : $A,B$ are any sets.

$|A| + |B|=|A\times \{0\}\cup B\times\{1\}|$
$|A|\cdot |B|=|A\times B|$
$\left|A^B\right| = |A|^{|B|}$
- Let $A^B$ denote $\{\alpha\mid \alpha:B\to A\text{ is a function}\}$ (the set of funtions from $B$ to $A$ )
  - We can informally refer to $n^A(n\in \mathbb{Z}^+)$ as $\{1,2,\cdots,n\}^{A}$

Let $a,b,c$ denote arbitrary cardinals, $\aleph_0$ is the cardinality of $\mathbb{Z}^+$, $c$ is the cardinality of $\mathbb{R}$.

Proposition :

$ab=ba$
$a(bc)=(ab)c$
$a(b+c)=ab+ac$
$b\le c\Rightarrow ab\le ac$
$a^2=a\cdot a$
$a^b\cdot a^c=a^{b+c}$
$(a^b)^c=a^{bc}$
$(ab)^c=a^c\cdot b^c$
$a^b\le 2^{ab}$
$a<2^a$
$\aleph_0+\aleph_0=\aleph_0$
$a\ge \aleph_0\Rightarrow a+ \aleph_0=a$
$\aleph_0\cdot \aleph_0=\aleph_0$
If $a$ is infinite cardinal, then $a^2=a$
If $b,c$ are infinite cardinals, then $b+c=bc=\max\{b,c\}$

Exercise

1.$\text { Let } A \text { and } B \text { be any sets. Show that } \mathcal{P}(A)=\mathcal{P}(B) \text { if and only if } A=B$

If $A=B$, then $\mathcal{P}(A)=\{x\mid x\subseteq A\}=\{x\mid x\subseteq B\}=\mathcal{P}(B)$.

If $A\ne B$ and we let $A\not\subset B$, then $\exist x, x\subseteq (A-B)\in \mathcal{P}(A) \text{ but }x\not\in \mathcal{P}(B)$. So $(A\ne B\Rightarrow \mathcal{P}(A)\ne \mathcal{P}(B)) \equiv (\mathcal{P}(A)=\mathcal{P}(B)\Rightarrow A=B)$.

So $(\mathcal{P}(A)=\mathcal{P}(B))\equiv (A=B)$.

2.$\text { Show that a set } S \text { is infinite if and only if there is a proper subset } A \subset S \text { such that } |A|=|S|$

If $S$ is an infinite set.
- If a set $S$ is a countably infinite set $\{a_1,a_2,...\}$, then let $A=\{a_2, a_3,...\}$ be a subset of $S$ . We can construct a bijection $f:S\to A\ a_i\mapsto a_{i+1}$, so $|A|=|S|$.
- if $S$ is a uncountably infinite set, we can let $S'=\{a_1,a_2,...\}$ be a countably infinite subset of $S$, then $A=\{a_2,a_3,...\}\cup (S-S')$ is a subset of $S$. We can construct a bijection $f:S\to A \begin{cases}a_i \mapsto a_{i+1}, &\text{if}\ \ a_{i}\in S'\\x\mapsto x, &\text{if}\ \ x\in(S-S')\end{cases}$
- So $|A|=|S|$ .
If $S$ is a finite set.
- Let $T$ be any subset of $S$ and $T\ne S$, then $|S|-|T|=|S-T|>0$.
- So $|A|\ne |S|$.

So we have proved that a set $S$ is infinite if and only if there is a proper subset $A\subset S$ such that $|A|=|S|$.

3.$\text{Prove or disprove the following statements: Let } A \text{ be any set of sets. Then } \cup \mathcal{P}(A)=A$.

If $\cup\mathcal{P}(A)\ne A$

If $|\cup \mathcal{P}(A)- A|=0$ , then there is a set $x\in A$ and $x\not\in \cup\mathcal{P}(A)$, but $A\in \mathcal{P}(A)$.
- This gives a contradiction.
If $|\cup\mathcal{P}(A)-A|>0$, then there is a set $x\in \cup\mathcal{P}(A)$ and $x\not\in A$, but $\mathcal{P}(A)=\{x\mid x\subseteq A\}$.
- This gives a contradiction.

4.$\text{Prove or disprove the following statements: Let } A \text{ be any set of sets. Then } \mathcal{P}(\cup A)=A$.

Let $A=\{\{1\},\{2\}\}$, then $\mathcal{P}(\cup A)=\{\empty,\{1\},\{2\},\{1,2\}\}\ne A$.

5.$\text { Prove or disprove }\left|\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2}=1\right\}\right|=|\mathbb{R}|$

Let $S= \{(x,y)\in \R^2:x^2+y^2=1\}$.

Construct an injection $f:S\to [0,1) \ \ (x,y)\mapsto (\cos\theta, \sin\theta)(\theta\in[0,2\pi))\mapsto \frac{\theta}{2\pi}$. So $|S|\le |[0,1)|$.
Construct an injection $g:[0,1)\to S\ \ x\mapsto (\cos2\pi x,\sin 2\pi x)$, so $|[0,1)|\le |S|$.

So $|S|=|[0,1)|=|\R|$.

6.$\text { Prove or disprove }\left|\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2}<1\right\}\right|=|\mathbb{R}|$

Let $S= \{(x,y)\in \R^2:x^2+y^2<1\}$.

Construct an injection $f:S \to [0,1)^2\ \ (x,y)\mapsto (x,y)$
- So $|S|\le|[0,1)^2|$
Construct an injection $g:[0,1)^2\to S\ \ (r,\theta)\mapsto (r\cos2\pi\theta, r\sin2\pi\theta)$
- So $|S|\ge |[0,1)^2|$

Accroding to $\textbf{Schröder-Bernstein Theorem}$, we can know $|S|=|[0,1)^2|$.

Accroding to Cardinal Arithmetic, we can know $|[0,1)^2|=|[0,1)|^2=|\R|^2=c^2=\left(2^{\aleph_0}\right)^2=2^{\aleph_0+\aleph_0}=2^{\aleph_0}=c=|\R|$.

So $|S|=|[0,1)^2|=|\R|$.

7.$\text { Prove or disprove }\left|\left\{A: A \subseteq \mathbb{Z}^{+},|A|<\infty\right\}\right|=\left|\mathbb{Z}^{+}\right|$

Let $S=\{A:A\subseteq \Z^+,|A|<\infty\}$, $M=\sup\{|A|: A\in S\}$.

Let $f:S\to \Z^+\ \ x=\{a_1,a_2,...,a_n\}(n\le M)\mapsto \sum\limits_{i=1}^{n}10^{a_i}$.
- So $|S|\le |\Z^+|$.
Let $g:\Z^+\to S\ \ x\to \{x\}$.
- So $|\Z^+|\le |S|$.

So $|S|=|\Z^+|$.

8.$\text { Prove or disprove }\left|\left\{\left(a_{1}, a_{2}, a_{3}, \ldots\right): a_{1}, a_{2}, a_{3}, \ldots \in \mathbb{Z}^{+}\right\}\right|=\left|\mathbb{Z}^{+}\right|$

Let $S=\left\{\left(a_{1}, a_{2}, a_{3}, \ldots\right): a_{1}, a_{2}, a_{3}, \ldots \in \mathbb{Z}^{+}\right\}$.

$\forall x\in [0, 1), x = 0.r_1r_2\cdots(r_1,r_2,\cdots\in\{0,...,9\},\text{no}\ \dot{9})$
- $0\leftrightarrow 0000,1\leftrightarrow 0001,...,9\leftrightarrow 1001$
- $x$ has a binary representation $x=0.b_1b_2\cdots$
  - $f:[0,1)\to S\ \ x\mapsto (a_1,a_2,\cdots)(i\in \Z^+\land b_{a_i}=1\land a_i<a_{i+1})\mapsto (a_1,a_2-a_1,a_3-a_2,\cdots)$.
  - So $|\Z^+|<|\R|=|[0,1)|\le |S|$

So $|\Z^+|<|S|$.

References

[1] Axiomatic Set Theory, University of Bristol, Charles Morgan
[2] Discrete Mathematics and Its Applications [7th Edition] - Kenneth H. Rosen
[3] Overview of basic results on cardinal arithmetic
[4] Lecture 5, Discrete Mathematics, SIST, STU
[5] Lecture 6, Discrete Mathematics, SIST, STU